Forecasting Walmart sales with Treeffuser

In this tutorial we show how to use Treeffuser to model and forecast Walmart sales using the M5 forecasting dataset from Kaggle.

Getting started

To get started, we first install treeffuser and import the relevant libraries.

%%capture
!pip install treeffuser

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from pathlib import Path

from tqdm import tqdm
from treeffuser import Treeffuser

# load autoreload extension
%load_ext autoreload
%autoreload 2

Next, create a Kaggle account and download the data from https://www.kaggle.com/competitions/m5-forecasting-accuracy/data.

If you’re running this notebook in Colab, manually upload the necessary files (calendar.csv, sales_train_validation.csv, sell_prices.csv) to Colab by clicking the Files tab on the left sidebar and selecting Upload. Move the files into a new folder named m5. Once uploaded, the notebook will be able to read and process the data.

If you’re running this on your local machine, you can also use Kaggle’s command-line tool and run the following from the command line:

cd ./m5 # path to folder where you want to save the data
kaggle competitions download -c m5-forecasting-accuracy

Use your favorite tool to unzip the archive. In Linux/macOS,

unzip m5-forecasting-accuracy.zip

We’ll be using the following files: calendar.csv, sales_train_validation.csv, and sell_prices.csv.

Load the data

data_path = Path("./m5")  # change with path where you extracted the data archive

calendar_df = pd.read_csv(data_path / "calendar.csv")
sales_train_df = pd.read_csv(data_path / "sales_train_validation.csv")
sell_prices_df = pd.read_csv(data_path / "sell_prices.csv")

# add explicit columns for the day, month, year for ease of processing
calendar_df["date"] = pd.to_datetime(calendar_df["date"])
calendar_df["day"] = calendar_df["date"].dt.day
calendar_df["month"] = calendar_df["date"].dt.month
calendar_df["year"] = calendar_df["date"].dt.year

The data

sell_prices_df contains the prices of each item in each store at a given time. The wm_yr_wk is a unique identifier for the time.

sell_prices_df.head()

	store_id	item_id	wm_yr_wk	sell_price
0	CA_1	HOBBIES_1_001	11325	9.58
1	CA_1	HOBBIES_1_001	11326	9.58
2	CA_1	HOBBIES_1_001	11327	8.26
3	CA_1	HOBBIES_1_001	11328	8.26
4	CA_1	HOBBIES_1_001	11329	8.26

calendar_df contains information about the dates on which the products were sold.

calendar_df.head()

	date	wm_yr_wk	weekday	wday	month	year	d	event_name_1	event_type_1	event_name_2	event_type_2	snap_CA	snap_TX	snap_WI	day
0	2011-01-29	11101	Saturday	1	1	2011	d_1	NaN	NaN	NaN	NaN	0	0	0	29
1	2011-01-30	11101	Sunday	2	1	2011	d_2	NaN	NaN	NaN	NaN	0	0	0	30
2	2011-01-31	11101	Monday	3	1	2011	d_3	NaN	NaN	NaN	NaN	0	0	0	31
3	2011-02-01	11101	Tuesday	4	2	2011	d_4	NaN	NaN	NaN	NaN	1	1	0	1
4	2011-02-02	11101	Wednesday	5	2	2011	d_5	NaN	NaN	NaN	NaN	1	0	1	2

sales_train_df contains the number of units sold for an item in each department and store. The sales are grouped by day: for example, the d_1907 column has the number of units sold on the 1907-th day.

sales_train_df.head()

	id	item_id	dept_id	cat_id	store_id	state_id	d_1	d_2	d_3	d_4	...	d_1904	d_1905	d_1906	d_1907	d_1908	d_1909	d_1910	d_1911	d_1912	d_1913
0	HOBBIES_1_001_CA_1_validation	HOBBIES_1_001	HOBBIES_1	HOBBIES	CA_1	CA	0	0	0	0	...	1	3	0	1	1	1	3	0	1	1
1	HOBBIES_1_002_CA_1_validation	HOBBIES_1_002	HOBBIES_1	HOBBIES	CA_1	CA	0	0	0	0	...	0	0	0	0	0	1	0	0	0	0
2	HOBBIES_1_003_CA_1_validation	HOBBIES_1_003	HOBBIES_1	HOBBIES	CA_1	CA	0	0	0	0	...	2	1	2	1	1	1	0	1	1	1
3	HOBBIES_1_004_CA_1_validation	HOBBIES_1_004	HOBBIES_1	HOBBIES	CA_1	CA	0	0	0	0	...	1	0	5	4	1	0	1	3	7	2
4	HOBBIES_1_005_CA_1_validation	HOBBIES_1_005	HOBBIES_1	HOBBIES	CA_1	CA	0	0	0	0	...	2	1	1	0	1	1	2	2	2	4

5 rows × 1919 columns

To align the sales data with the other DataFrames, we convert sales_train_df to a long format. We collapse the daily sales columns d_{i} into a single sales column, with an additional day column indicating the day corresponding to each sales entry.

def convert_sales_data_from_wide_to_long(sales_df_wide):
    index_vars = ["item_id", "dept_id", "cat_id", "store_id", "state_id"]
    sales_df_long = pd.wide_to_long(
        sales_df_wide.iloc[:100, 1:],
        i=index_vars,
        j="day",
        stubnames=["d"],
        sep="_",
    ).reset_index()

    sales_df_long = sales_df_long.rename(columns={"d": "sales", "day": "d"})

    sales_df_long["d"] = "d_" + sales_df_long["d"].astype(
        "str"
    )  # restore "d_{i}" format for day
    return sales_df_long


sales_train_df_long = convert_sales_data_from_wide_to_long(sales_train_df)
sales_train_df_long.head()

	item_id	dept_id	cat_id	store_id	state_id	d	sales
0	HOBBIES_1_001	HOBBIES_1	HOBBIES	CA_1	CA	d_1	0
1	HOBBIES_1_001	HOBBIES_1	HOBBIES	CA_1	CA	d_2	0
2	HOBBIES_1_001	HOBBIES_1	HOBBIES	CA_1	CA	d_3	0
3	HOBBIES_1_001	HOBBIES_1	HOBBIES	CA_1	CA	d_4	0
4	HOBBIES_1_001	HOBBIES_1	HOBBIES	CA_1	CA	d_5	0

plt.hist(
    sales_train_df_long["sales"],
    bins=np.arange(0, 10 + 1.5) - 0.5,
    range=[0, 10],
    density=True,
)
plt.xticks(range(10))
plt.ylabel("Frequency of number of sales")
plt.title("Number of sales over the entire timespan")

Text(0.5, 1.0, 'Number of sales over the entire timespan')

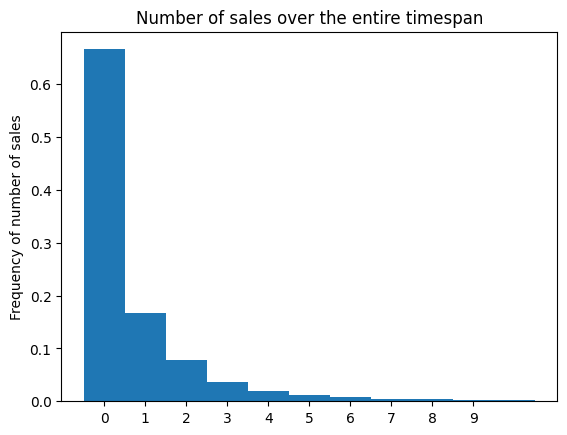
The dataset comprises sales data of 100 items over 1,913 days. For simplicity, we select the data from the first 365 days and discard the rest.

print(f"n_items = {len(sales_train_df_long['item_id'].unique())}")
print(f"n_days = {len(sales_train_df_long['d'].unique())}")

sales_train_df_long["day_number"] = sales_train_df_long["d"].str.extract("(\d+)").astype(int)
data = sales_train_df_long[sales_train_df_long["day_number"] <= 365].copy()

n_items = 100
n_days = 1913

We compute the lags of the previous 30 days and merge the sales, calendar, and price data together.

n_lags = 30

# sort data before computing lags
data_index_vars = ["item_id", "dept_id", "cat_id", "store_id", "state_id"]
data.sort_values(data_index_vars + ["day_number"], inplace=True)

for lag in range(1, n_lags + 1):
    data[f"sales_lag_{lag}"] = data.groupby(by=data_index_vars)["sales"].shift(lag)

data = data.merge(calendar_df).merge(sell_prices_df)

data.head()

	item_id	dept_id	cat_id	store_id	state_id	d	sales	day_number	sales_lag_1	sales_lag_2	...	year	event_name_1	event_type_1	event_name_2	event_type_2	snap_CA	snap_TX	snap_WI	day	sell_price
0	HOBBIES_1_002	HOBBIES_1	HOBBIES	CA_1	CA	d_141	0	141	0.0	0.0	...	2011	NaN	NaN	NaN	NaN	0	0	0	18	3.97
1	HOBBIES_1_002	HOBBIES_1	HOBBIES	CA_1	CA	d_142	0	142	0.0	0.0	...	2011	Father's day	Cultural	NaN	NaN	0	0	0	19	3.97
2	HOBBIES_1_002	HOBBIES_1	HOBBIES	CA_1	CA	d_143	0	143	0.0	0.0	...	2011	NaN	NaN	NaN	NaN	0	0	0	20	3.97
3	HOBBIES_1_002	HOBBIES_1	HOBBIES	CA_1	CA	d_144	1	144	0.0	0.0	...	2011	NaN	NaN	NaN	NaN	0	0	0	21	3.97
4	HOBBIES_1_002	HOBBIES_1	HOBBIES	CA_1	CA	d_145	0	145	1.0	0.0	...	2011	NaN	NaN	NaN	NaN	0	0	0	22	3.97

5 rows × 53 columns

Treeffuser can handle categorical columns, but the dtype of those columns must be set to category in the DataFrame.

categorical_columns = [
    "item_id",
    "dept_id",
    "cat_id",
    "store_id",
    "state_id",
    "d",
    "wm_yr_wk",
    "weekday",
    "event_name_1",
    "event_type_1",
    "event_name_2",
    "event_type_2",
    "snap_CA",
    "snap_TX",
    "snap_WI",
]
data[categorical_columns] = data[categorical_columns].astype("category")

Finally, for each item, we take the first 300 days as train data and use the remaining 65 data as test data for evaluation.

is_train = data["day_number"] <= 300

y_name = "sales"
x_names = [
    name for name in data.columns if name != y_name and name not in ["day_number", "date"]
]

X_train, y_train, dates_train = (
    data[is_train][x_names],
    data[is_train][y_name],
    data[is_train]["date"],
)
X_test, y_test, dates_test = (
    data[~is_train][x_names],
    data[~is_train][y_name],
    data[~is_train]["date"],
)

print(X_train.shape)
print(X_test.shape)

(15216, 50)
(3891, 50)

Probabilistic predictions with Treeffuser

We regress the sales on the following covariates.

print(", ".join(map(str, X_train.columns)))

item_id, dept_id, cat_id, store_id, state_id, d, sales_lag_1, sales_lag_2, sales_lag_3, sales_lag_4, sales_lag_5, sales_lag_6, sales_lag_7, sales_lag_8, sales_lag_9, sales_lag_10, sales_lag_11, sales_lag_12, sales_lag_13, sales_lag_14, sales_lag_15, sales_lag_16, sales_lag_17, sales_lag_18, sales_lag_19, sales_lag_20, sales_lag_21, sales_lag_22, sales_lag_23, sales_lag_24, sales_lag_25, sales_lag_26, sales_lag_27, sales_lag_28, sales_lag_29, sales_lag_30, wm_yr_wk, weekday, wday, month, year, event_name_1, event_type_1, event_name_2, event_type_2, snap_CA, snap_TX, snap_WI, day, sell_price

model = Treeffuser(seed=0)
model.fit(X_train, y_train)

[LightGBM] [Warning] Met negative value in categorical features, will convert it to NaN
[LightGBM] [Warning] Met negative value in categorical features, will convert it to NaN
[LightGBM] [Warning] Met negative value in categorical features, will convert it to NaN
[LightGBM] [Warning] Met negative value in categorical features, will convert it to NaN
[LightGBM] [Warning] Categorical features with more bins than the configured maximum bin number found.
[LightGBM] [Warning] For categorical features, max_bin and max_bin_by_feature may be ignored with a large number of categories.

Treeffuser(extra_lightgbm_params={}, seed=0)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

y_test_samples = model.sample(X_test, n_samples=100, seed=0, n_steps=50, verbose=True)

100%|██████████| 100/100 [05:55<00:00,  3.55s/it]

Newsvendor model

We illustrate the practical relevance of accurate probabilistic predictions with an application to inventory management, using the newsvendor model \citep{arrow1951optimal}.

Assume that every day we decide how many units \(q\) of an item to buy. We buy at a cost \(c\) and sell at a price \(p\). However, the demand \(y\) is random, introducing uncertainty in our decision. The goal is to maximize the expected profit:

\[\max_{q} p~\mathbb{E}\left[\min(q, y)\right] - c q.\]

The optimal solution to the newsvendor problem is to buy \(q = F^{-1}\left( \frac{p-c}{p} \right)\) units, where \(F^{-1}\) is the quantile function of the distribution of \(y\).

Using Treeffuser, we can compute the quantiles from the samples and forecast the optimal quantity of units to buy.

To compute profits, we use the observed prices, assume a margin of \(50\%\) over all products, and assume the actual number of sales of an item correspond to the demand of this item. We let Treeffuser, learn the conditional distribution of the demand of each item, estimate their quantiles, and thus determine the optimal quantity to buy.

We use the held-out data to compute the profit made if Treeffuser was used to forecast the demand of each item and to manage the inventory of each item.

def newsvendor_utility(y_true, quantity_ordered, prices, stocking_cost):
    """
    The newsvendor utility function with stock q, demand y, selling price p, stocking cost c is given by
    $$ U(y, q, p, c) = p * min(y, q) - c * q $$
    """
    utility = prices * np.minimum(y_true, quantity_ordered) - stocking_cost * quantity_ordered
    return utility


def newsvendor_optimal_quantity(y_samples, prices, stocking_cost):
    """
    Returns the optimal quantity to order for the newsvendor problem.

    It is given theoeretically by:
        $$ q* = argmax_{q} E[U(y, q, p, c)] $$
    which has a closed form solution,
        $$ q* = F^{-1}( (p - c) / p) $$
    where F is the CDF of the demand distribution
    """
    # compute the target quantiles (p - c) / p
    target_quantiles = (prices - stocking_cost) / prices
    target_quantiles = np.maximum(target_quantiles, 0.0)

    # compute the empirical quantities corresponding to the target quantiles
    res = []
    for i in range(y_samples.shape[1]):
        optimal_quantities = np.quantile(y_samples[:, i], target_quantiles[i])
        res.append(optimal_quantities)
    optimal_quantities = np.array(res)
    return optimal_quantities

# we don't know the profit margin of each item, so we assume it is 50%.
profit_margin = 0.5

prices = X_test["sell_price"].values
stocking_cost = prices / (1 + profit_margin)

# compute optimal quantities
optimal_quantities = newsvendor_optimal_quantity(y_test_samples, prices, stocking_cost)

# Treeffuser models continuous responses, hence we cast the predicted quantities into int
optimal_quantities = optimal_quantities.astype(int)

profit = newsvendor_utility(y_test, optimal_quantities, prices, stocking_cost)
profit.sum()

185.07666666666668

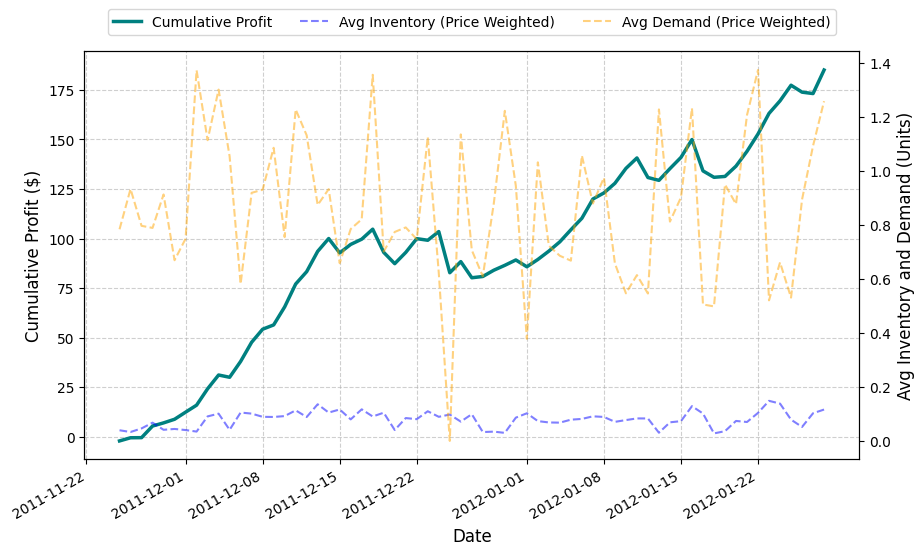
We visualize the cumulative profit, the average demand and inventory over time in the plot below.

performance_data = pd.DataFrame(
    {
        "date": dates_test,
        "profit": profit,
        "demand": y_test,
        "inventory": optimal_quantities,
        "price": prices,
    }
)

# for each day, compute average demand and inventory weighted by price
daily_summary = (
    performance_data.groupby("date")
    .agg(
        profit=("profit", "sum"),
        avg_inventory_weighted=(
            "inventory",
            lambda x: (x * performance_data.loc[x.index, "price"]).sum()
            / performance_data.loc[x.index, "price"].sum(),
        ),
        avg_demand_weighted=(
            "demand",
            lambda x: (x * performance_data.loc[x.index, "price"]).sum()
            / performance_data.loc[x.index, "price"].sum(),
        ),
    )
    .reset_index()
)

print(daily_summary)

         date     profit  avg_inventory_weighted  avg_demand_weighted
0  2011-11-25  -2.213333                0.039476             0.784104
1  2011-11-26   1.600000                0.033068             0.933309
2  2011-11-27   0.053333                0.046308             0.796895
3  2011-11-28   5.873333                0.067636             0.789166
4  2011-11-29   1.580000                0.041286             0.913090
..        ...        ...                     ...                  ...
60 2012-01-24   6.336667                0.138240             0.661504
61 2012-01-25   7.876667                0.078847             0.530883
62 2012-01-26  -3.493333                0.051774             0.894360
63 2012-01-27  -0.710000                0.102579             1.093555
64 2012-01-28  11.890000                0.116262             1.258714

[65 rows x 4 columns]

# dictionary to store color, alpha, linewidth, and linestyle for each line
line_styles = {
    "cumulative_profit": {"color": "teal", "alpha": 1, "linewidth": 2.5, "linestyle": "-"},
    "inventory": {
        "color": "blue",
        "alpha": 0.5,
        "linewidth": 1.5,
        "linestyle": "--",
    },
    "demand": {
        "color": "orange",
        "alpha": 0.5,
        "linewidth": 1.5,
        "linestyle": "--",
    },
}

# create figure
fig, ax1 = plt.subplots(figsize=(10, 6))

# define x-axis
dates = pd.to_datetime(daily_summary["date"])

# plot cumulative profit
ax1.plot(
    dates,
    daily_summary["profit"].cumsum(),
    **line_styles["cumulative_profit"],
    label="Cumulative Profit",
)
ax1.set_xlabel("Date", fontsize=12)
ax1.set_ylabel("Cumulative Profit ($)", fontsize=12)
ax1.grid(True, linestyle="--", alpha=0.6)

# create second y-axis for price-weighted inventory and demand
ax2 = ax1.twinx()
ax2.plot(
    dates,
    daily_summary["avg_inventory_weighted"],
    **line_styles["inventory"],
    label="Avg Inventory (Price Weighted)",
)
ax2.plot(
    dates,
    daily_summary["avg_demand_weighted"],
    **line_styles["demand"],
    label="Avg Demand (Price Weighted)",
)
ax2.set_ylabel("Avg Inventory and Demand (Units)", fontsize=12)

# combine all legends into one
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax1.legend(
    lines1 + lines2, labels1 + labels2, loc="upper center", bbox_to_anchor=(0.5, 1.12), ncol=3
)

fig.autofmt_xdate()  # rotate x-tick labels

plt.show()